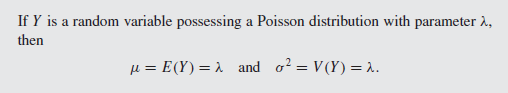Poisson Distribution

What is the Poisson Distribution?

Technical Definition

Recall that a distribution is a set of weights that sum up to one, ie $\Sigma w_{i}$ The Poisson distribution is a probability distribution where each weight is the probability of a particular event.
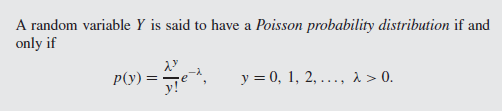
Definition of Poisson Distribution

Where Do We See the Poisson Distribution?

The Poisson distribution is often used to model the number of events that occur independently at any time in an interval of time or space with a constant average.
Consider this problem. Let’s assume a big earthquake strikes San Francisco on average once ever 100 years. How do we calculate the probability of $k=3$ earthquakes occuring in a 200-year interval.
At first, we may think $K~Binomial(n=100, p=1/100)$ ; however, that assumes that only one earthquake may occur in a given year. $n$ is the number of intervals and we need our intervals to be so small that the probability of more than one earthquake in an interval iszero.. We need to make our intervals so small that the probability of more than one earthquake in an interval iszero.. We need our intervals to be infinitely small, $n\rightarrow \infty$
When we set the limit as $n → \infty$ , we get an idealization called a Poisson Process.
Definition of Poisson Process

Poisson Distribution Approximates Binomial Distribution

The Poisson Distribution is a useful approximation for the binomial distribution when the sample size ( $n$ ) is large or $p$ is small.
Consider this problem.
Let’s say you want to send a bit string of length $n = 104$ where each bit is independently corrupted with $p = 10^{−6}$ . What is the probability that the message will arrive uncorrupted? You can solve this using a Poisson with $λ = np = 104 \times 10^{−6} = 0.01$ . Let $X ∼ Poi(0.01)$ be the number of corrupted bits. Using the PMF for Poisson:
$P(X = 0) = \frac{λ^{x}e^{−λ}}{x!} ≈ 0.9900498$
We could have also modeled X as a binomial such that $X ∼ Bin(104, 10^{−6})$ . That would have been harder to compute but would have resulted in the same number (to 8 decimal places).

Expectation and Variance of Poisson Random Variable

A cool feature of the Poisson Random Variable is that it’s expectation and variance both equal $\lambda$ .